comp-library
This documentation is automatically generated by online-judge-tools/verification-helper
 円と円の交差判定
円と円の交差判定
(src/geometry/Z2/intersect/is-intersect-circle-circle.hpp)
- View this file on GitHub
- Last update: 2022-08-22 19:09:09+09:00
- Include:
#include "src/geometry/Z2/intersect/is-intersect-circle-circle.hpp"
is_intersect_cc
bool is_intersect_cc(Z2::Circle<Z> c0, Z2::Circle<Z> c1)
円 c0 と c1 が交差しているかどうかを返す。
制約
- 中心座標間の距離の2乗が
Z上でオーバーフローしないこと。 - 半径の和の2乗が
Z上でオーバーフローしないこと。
解説
2つの円が交点を持たないのは以下の2通り。
- 一方の円がもう一方の円に内包されている場合
- 円周も面積も共有しない場合
1 の場合、$(中心間の距離 + 小さいほうの半径) < 大きいほうの半径$ が条件である。
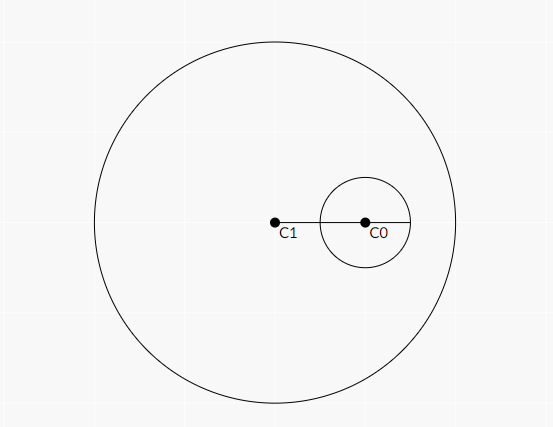
2 の場合、$(中心間の距離 - 一方の半径) > もう一方の半径$ が条件となる。
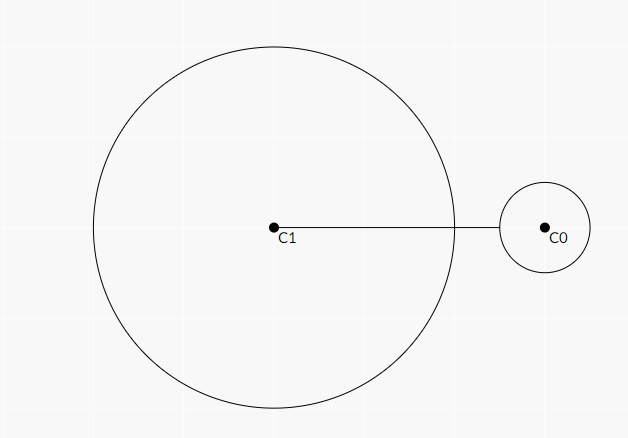
距離や半径の計算には sqrt が出てくるが、式を整理して2乗して扱うことで整数上で考えることができ、誤差なく交差判定を扱うことができる。
Depends on
 円 (整数幾何)
(src/geometry/Z2/class/circle.hpp)
円 (整数幾何)
(src/geometry/Z2/class/circle.hpp)
 格子点 (整数幾何)
(src/geometry/Z2/class/point.hpp)
格子点 (整数幾何)
(src/geometry/Z2/class/point.hpp)
 ベクトル (整数幾何)
(src/geometry/Z2/class/vector.hpp)
ベクトル (整数幾何)
(src/geometry/Z2/class/vector.hpp)
 $\|v\|^2 (v \in {\mathbb{Z}}^2)$ (normの2乗)
(src/geometry/Z2/operation/square-norm.hpp)
$\|v\|^2 (v \in {\mathbb{Z}}^2)$ (normの2乗)
(src/geometry/Z2/operation/square-norm.hpp)
 $x^2 (x \in \mathbb{Z})$
(src/geometry/Z2/operation/square.hpp)
$x^2 (x \in \mathbb{Z})$
(src/geometry/Z2/operation/square.hpp)
Verified with
Code
#pragma once
#include "src/geometry/Z2/class/circle.hpp"
#include "src/geometry/Z2/class/point.hpp"
#include "src/geometry/Z2/operation/square-norm.hpp"
#include "src/geometry/Z2/operation/square.hpp"
#include <utility>
namespace luz::Z2 {
template < typename Z >
bool is_intersect_cc(Circle< Z > c0, Circle< Z > c1) {
if (c0.r() > c1.r()) std::swap(c0, c1);
Z sq_dist = square_norm(c0.center() - c1.center());
if (sq_dist < square(c1.r() - c0.r())) return false;
if (square(c1.r() + c0.r()) < sq_dist) return false;
return true;
}
} // namespace luz::Z2#line 2 "src/geometry/Z2/intersect/is-intersect-circle-circle.hpp"
#line 2 "src/geometry/Z2/class/circle.hpp"
#line 2 "src/geometry/Z2/class/point.hpp"
#line 2 "src/geometry/Z2/class/vector.hpp"
#include <vector>
namespace luz::Z2 {
template < typename Z >
class Vector {
Z x_, y_;
public:
Vector(): x_(0), y_(0) {}
Vector(Z x, Z y): x_(x), y_(y) {}
Z x() const {
return x_;
}
Z y() const {
return y_;
}
bool operator==(const Vector &v) const {
return x_ == v.x_ and y_ == v.y_;
}
bool operator!=(const Vector &v) const {
return x_ != v.x_ or y_ != v.y_;
}
Vector &operator+=(const Vector &v) {
x_ += v.x_;
y_ += v.y_;
return *this;
}
Vector &operator-=(const Vector &v) {
x_ -= v.x_;
y_ -= v.y_;
return *this;
}
Vector operator+(const Vector &v) const {
return Vector(*this) += v;
}
Vector operator-(const Vector &v) const {
return Vector(*this) -= v;
}
Vector operator+() const {
return *this;
}
Vector operator-() const {
return Vector() - *this;
}
};
template < typename Z >
using Vectors = std::vector< Vector< Z > >;
} // namespace luz::Z2
#line 4 "src/geometry/Z2/class/point.hpp"
#line 6 "src/geometry/Z2/class/point.hpp"
namespace luz::Z2 {
template < typename Z >
using Point = Vector< Z >;
template < typename Z >
using Points = std::vector< Point< Z > >;
} // namespace luz::Z2
#line 4 "src/geometry/Z2/class/circle.hpp"
#include <cassert>
namespace luz::Z2 {
template < typename Z >
class Circle {
Point< Z > o_;
Z r_;
public:
Circle(): o_(0, 0), r_(0) {}
Circle(Point< Z > o, Z r): o_(o), r_(r) {
assert(r >= 0);
}
Point< Z > center() const {
return o_;
}
Z r() const {
return r_;
}
};
template < typename Z >
using Circles = std::vector< Circle< Z > >;
} // namespace luz::Z2
#line 2 "src/geometry/Z2/operation/square-norm.hpp"
#line 2 "src/geometry/Z2/operation/square.hpp"
namespace luz::Z2 {
template < typename Z >
Z square(const Z x) {
return x * x;
}
} // namespace luz::Z2
#line 5 "src/geometry/Z2/operation/square-norm.hpp"
namespace luz::Z2 {
template < typename Z >
Z square_norm(Vector< Z > v) {
return square(v.x()) + square(v.y());
}
} // namespace luz::Z2
#line 7 "src/geometry/Z2/intersect/is-intersect-circle-circle.hpp"
#include <utility>
namespace luz::Z2 {
template < typename Z >
bool is_intersect_cc(Circle< Z > c0, Circle< Z > c1) {
if (c0.r() > c1.r()) std::swap(c0, c1);
Z sq_dist = square_norm(c0.center() - c1.center());
if (sq_dist < square(c1.r() - c0.r())) return false;
if (square(c1.r() + c0.r()) < sq_dist) return false;
return true;
}
} // namespace luz::Z2